이 글은 Qiskit 공식 홈페이지에서 제공하는 튜토리얼을 직접 해보고 요약하거나 덧붙이거나 교정한 글입니다. 원문은 [1]이며, Anaconda 의 Jupyter notebook 을 사용하는 원문과 달리 순수 Python 으로 실행가능하도록 소스코드를 수정하고, 중간마다 양자 상태를 시각화하는 코드 등이 추가되어 코드도 원문과 차이가 있습니다. 제가 작성한 코드는 [2]에 공개합니다.
이 단원에서는 Qiskit Terra 에서 이용 가능한 여러가지 연산들에 대하여 다룬다. 목록은 다음과 같다.
- 단일 큐비트 양자 게이트
- 다중 큐비트 양자 게이트
- 측정
- 초기화 (Reset)
- 조건
- 상태 초기화
또한 세 가지 종류의 시뮬레이터를 사용하는 방법도 설명한다.
- unitary_simulator
- qsam_simulator
- statevector_simulator
우선 다음의 기본 import 와 백엔드 선언으로 코드를 시작한다.
3.1. 단일 큐비트 양자 상태
단일 큐비트 양자 상태는 다음과 같이 기술할 수 있다.
|ψ〉 = α |0〉 + β |1〉
여기서 α 와 β 는 복소수이다. 측정에서 큐비트가 |0〉에 있을 확률은 |α|² 이고, |1〉일 확률은 |β|² 이다. 백터를 행렬로 표현하면 아래와 같다.
확률의 보존으로 인해 |α|² + |β|² = 1 이며, 전역 위상이 감지되지 않는 |ψ〉 := eiδ |ψ〉이므로, 단일 큐비트 양자 상태를 설명하기 위해 두 개의 실수만 필요하다. 전역 위상이 Φ 와 θ 일 때 다음과 같이 나타낼 수 있다.
|ψ〉 = cos(θ/2) |0〉 + sin(θ/2) eiΦ |1〉
여기에서 0 ≤ Φ ≤ 2π 이고, 0 ≤ θ ≤ π 이다. 물론 큐비프 상태(C²) 와 단위 구 표면의 점(R³)은 일대일로 대응된다. 이를 큐비트 상태의 블로흐 구체 표현이라고 한다.
양자 게이트 / 연산은 일반적으로 행렬로 표현한다. 특히 큐비트에 작용하는 게이트는 2 x 2 유니타리 행렬 U 로 표현된다. 그리고 양자 게이트의 작용은 양자 상태를 나타내는 벡터에 게이트를 나타내는 행렬을 곱함으로써 알 수 있다.
|ψ‘〉 = U |ψ〉
일반적으로 유니타리 상태에서는 |0〉을 위의 상태로만들 수 있어야 한다. 따라서 U는 다음과 같다.
여기에서 a와 b는 임의로 주어진 0 ≤ θ ≤ π 와 0 ≤ Φ ≤ 2π 에 대해 U†U = I 를 만족하는 복소수이다. (여기에서 † 는 영어로 '대거(dagger)' 라고 읽는다. 우리말로는 '칼표' 라고 부른다. U† 는 행렬 U 의 i 행 j 열 위치의 원소를 j 행 i 열로 이동(전치)시키고, 복소수 i 들의 ± 부호를 뒤집어서(켤레) 만든 행렬이다. 자세한 내용은 위키[3] 참고) 또, 0 ≤ λ ≤ 2π 일 때, a → -eiλ sin(θ/2) 와 b → eiλ+iΦ cos(θ/2) 인 세 가지 제약조건을 준다. 따라서 다음과 같다.
이는 단일 큐비트에 작용되는 유니타리의 가장 일반적인 형태이다.
3.2. 단일 큐비트 게이트들
사용할 수 있는 단일 큐비트 게이트는 U게이트들, 항등(Identity) 게이트, 파울리(Pauli) 게이트, 클리포드(Clifford) 게이트, C3 게이트, 표준 회전(Standard rotation) 게이트이다. 키스킷은 유니타리 행렬들을 계산할 수 있는 unitary_simulator 백엔드를 제공한다.
다음의 코드로 단일 큐비트 회로를 생성하고, 초기 상태를 살펴본다.
3.2.1. U 게이트들
3.2.1.1. U3 게이트
Qiskit 에서는 일반적인 유니타리 연산을 사용할 수 있도록 u3 게이트를 제공한다.
코드 35번 라인에서 유니타리 행렬을 출력한 결과는 다음과 같다.
[ 0.+0.707j -0.707+0.j]]
위 출력 결과에서 j는 python의 복소수 i 표기이며, 0.707은 1/√2의 근사값이다. 즉, 다음의 행렬이다.
3.2.1.2. U2 게이트
u2 게이트는 u3 게이트로 u2(Φ, λ) =u3(π/2, Φ, λ)이며, 다음의 행렬로도 표현된다.
이것은 우리가 중첩을 만들 수 있게 해주는 유용한 게이트이다.
3.2.1.3. U1 게이트
u1 게이트는 u3 게이트로 표현하면 u1(λ) = u3(0, 0, λ)이며, 행렬로는 다음과 같다.
이 게이트는 양자 위상을 만들어주므로 유용하다.
u1게이트는 파동의 위상만 변경하여, 단일 큐비트의 상태벡터에는 영향을 미치지 않는다. 코드 59번 라인의 실행 결과는 다음과 같다.
3.2.2. 항등(Identity) 게이트
항등 게이트는 Id는 u0(1) 과 같다. 즉, Id = u(0).
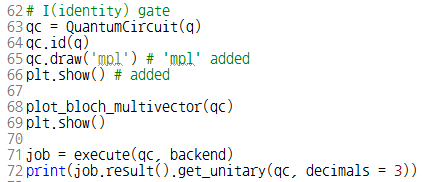
항등 게이트는 큐비트의 상태 벡터에 영향을 주지 않는다. 코드 71번 라인의 출력 결과는 다음과 같다.
3.2.3. 파울리(Pauli) 게이트들
3.2.3.1. X 게이트
비트 플립 게이트이며, 다음의 수식과 같이 정의된다.
Qiskit 구현은 다음과 같다.
코드 80번 라인을 통해 회로를 출력하면 다음과 같다.
코드 83번 라인으로 큐비트의 상태벡터를 도식하면 다음과 같이 비트가 플립된다.
3.2.3.2. Y 게이트
비트와 위상을 플립하는 게이트이며, 다음의 수식으로 정의된다.
회로의 구현은 다음과 같다.
코드 92번 라인의 결과로 아래와 같이 출력된다.
코드 95번 라인의 결과로 아래와 같이 블로흐 구에서 비트가 플립된 것을 볼 수 있다.
코드 98번 라인의 결과는 상기 수식과 동일하다.
3.2.3.3. Z 게이트
위상 플립 게이트 Z는 다음의 수식으로 정의된다.
Z 게이트의 회로는 다음과 같이 구현할 수 있다.
코드 105번 라인의 결과는 다음과 같다.
코드 108번 라인은 다음의 블로흐 구를 도식한다. 위상만 변경되어 비트는 유지된다.
코드 111번 라인의 결과는 앞의 수식과 같다.
3.2.4. 클리포드(Clifford) 게이트들
3.2.4.1. 하마다드(Hadamard) 게이트
이 게이트는 단일 큐비트를 0과 1의 중첩 상태로 만든다. 수식은 다음과 같다.
회로의 구현은 다음과 같다.
코드 118번 라인의 출력 결과는 다음과 같다.
코드 121번 라인의 출력 결과는 다음과 같다.
코드 124번의 출력 결과는 다음과 같다. 수식과 동일함을 알 수 있다.
3.2.4.2. S (또는 √Z 위상) 게이트
이 게이트는 양자 위상을 π/2 만큼 수정한다. 수식은 다음과 같다.
회로의 구현은 다음과 같다.
코드 130 라인의 출력은 다음과 같다.
코드 133번 라인의 출력은 다음과 같다.
코드136번 라인의 출력은 다음과 같다.
3.2.4.2. S† (또는 √Z 위상의 켤레) 게이트
수식은 다음과 같다.
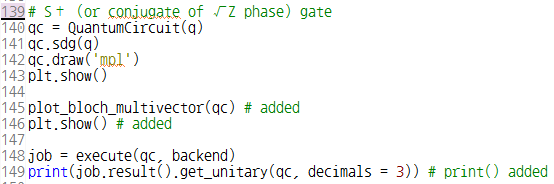
회로의 구현은 다음과 같다.
코드 143번 라인의 출력은 다음과 같다.
코드 146번 라인의 출력은 다음과 같다.
코드 149번 라인의 출력은 다음과 같다.
3.2.5. C3 게이트들
3.2.5.1. T (또는 √S 위상) 게이트
수식은 다음과 같다.
구현은 다음과 같다.
코드 157번 라인의 출력은 다음과 같다.
코드 160번 라인의 출력은 다음과 같다.
코드 163번 라인의 출력은 다음과 같다.
32.5.2. T† (또는 √S 위상의 켤레) 게이트
수식은 다음과 같다.
양자 회로의 구현은 다음과 같다.
코드 169번 라인의 출력은 다음과 같다.
코드 172번 라인의 출력은 다음과 같다.
코드 176번 라인의 출력은 다음과 같다.
3.2.6. 표준 회전들
표준 회전 게이트들은 파울리 P = {X, Y, Z}에 대응하는 블로흐 벡터 축을 기준으로 하는 회전을 정의하는 게이트이다. 수식으로 다음과 같이 정의된다.
3.2.6.1. X축에 대한 회전 게이트
수식은 다음과 같다.
회로의 구현은 다음과 같다.
코드3.14. Rx 게이트 회로 구현
코드 184번 라인의 출력은 다음과 같다.
코드 187번 라인의 출력은 다음과 같다.
3.2.6.2. Y축에 대한 회전 게이트
수식은 다음과 같다.
회로의 구현은 다음과 같다.
코드 197번 라인의 출력은 다음과 같다.
코드 200번 라인의 출력은 다음과 같다.
코드 203번 라인의 출력은 다음과 같다.
3.2.6.3. Z축에 대한 회전 게이트
수식은 다음과 같다.
여기에서 전역 위상만 e-iΦ/2 만큼 차이난다는 의미에서 동치를 사용하였다. 구현은 다음과 같다.
코드 210번 라인의 출력은 다음과 같다.
코드 213번 라인의 출력은 다음과 같다.
코드 216번 라인의 출력은 다음과 같다. 오직 전역 위상만 다르다.
3.3. 다중 큐비트 게이트
3.3.1. 수학적 예비
양자 컴퓨터를 기술하는 공간의 차원은 큐비트의 개수가 증가함에 따라 지수적으로 증가한다. n 큐비트를 기술하는 복소 벡터 공간은 2ⁿ 차원을 가지기 때문이다. 다중 큐비트 시스템의 상태를 표현할 때는 텐서곱을 사용하여 연산자들이나 기저 벡터 사이를 붙여줄 수 있다.
우선 두 개의 큐비트들로 구성된 시스템을 생각해보자. 각 큐비트에서 작용하는 두 개의 연산자 A 와 B 가 주어졌을 때 두 개의 큐비트에 동시에 작용하는 연합 연산자 A⊗B 는 다음과 같다.
여기서 Ajk 와 Blm 은 각각 A 행렬과 B 행렬의 성분이다. 이와 유사하게, 두 큐비트 시스템의 기저 벡터들은 단일 큐비트의 기저 벡터들을 텐서곱하여 형성된다.
기저 벡터의 텐서곱 |0〉⊗|0〉는 |00〉로 간략하게 쓸 수 있다. n 큐비트 시스템의 상태는 단일 큐비트 기저 벡터들을 n 번 텐서곱하여 표현할 수 있다. 2큐비트 시스템의 기저 벡터의 차원은 4차원이며, n 큐비트 시스템의 기저 벡터의 차원은 2ⁿ임을 기억하자.
3.3.1.1. 키스킷에 사용되는 기저 벡터의 순서
물리학에서 다중 큐비트 시스템의 큐비트들을 나열할 때 대부분 첫 번째 큐비트를 텐서곱의 가장 왼쪽에 놓고, 마지막 큐비트를 가장 오른쪽에 놓는 순서를 따른다. 예를 들어, 첫 번째 큐비트의 상태가 |0〉이고, 두 번째 큐비트의 상태가 |1〉이면, 전체 상태는 |01〉이 된다. 키스킷은 조금 다른 순서로큐비트를 나열하는데 가장 중요한 비트(MSB)가 좌측에 있고, 가장 덜 중요한 비트(LSB)가 우측에 놓이는 big-endian 방식을 따른다. 이는 전통적인 컴퓨터에서 사용되는 비트열 표현과 비슷하며, 측정을 한 후에 문자열을 정수로 변환하는 과정을 쉽게 만든다. 앞선 예의 경우 전체 상태는 |10〉로 표현된다. 중요한 점은 이러한 다중 큐비트 상태의 표기법의 차이가 Qiskit 에서 표현되는 다중 큐비트 게이트를 나타내느 방법에 변화를 준다는 것이다. 다음을 살펴보자.
키스킷에서 사용하는 표현은 기저 벡터를 표현하는 숫자가 증가하는 순으로 번호를 매긴다. 예를 들어 두 큐비트 시스템의 기저 벡터들은 |00〉, |01〉, |10〉, |11〉 순으로 배열된다. 이때 기저 벡터에 대응하는 비트열을 살펴보면 각각 0, 1, 2, 3이 인코딩되어 있다.
3.3.1.2. 큐비트에 적용되는 제어 연산들
일반적인 다중 큐비트 게이트는 한 큐비트에 가하는 게이트나 다른 큐비트에 조건부로 작용하는 게이트와 그 응용을 모두 포함한다. 예를 들어 첫 번째 큐빗이 |0〉일 떄 두 번째 큐비트가 플립되는 게이트를 고려하자. 이러한 게이트는 제어 게이트들(controlled gates)로 알려져 있다. 표준 다중 큐비트 게이트는 두 큐비트 게이트와 세 큐비트 게이트로 구성되어 있는데 두 큐비트 게이트에는 제어 파울리 게이트들(controlled pauli gates), 제어 하다마드 게이트(controlled hadamard gate), 제어 회전 게이트들(controlled rotation gates), 제어 위상 게이트(controlled phase gate), 제어 u3 게이트(controlled u3 gate), 교환 게이트(swap gate)가 있으며, 세 큐비트 게이트에는 토폴리 게이트(Toffoli gate)와 프레드킨 게이트(또는 제어 교환 게이트, Fredkin gate or Controlled swap gate)가 있다.
3.3.2. 두 큐비트 게이트들(Two-qubit gates)
Swap 게이트를 제외하면, 대부분의 두 큐비트 게이트들은 다른 큐비트에 의헤 제어되는 유형이다. 일반적으로 다른 큐비트에 의해 제어되는 두 큐비트 게이트 CU 는 첫 번째 큐비트의 상태가 |1〉일 때 단일 큐비트 유니타리 U를 두 번째 큐비트에 가하는 식이다. 유니타리 U 가 다음의 행렬이라고 가정하자.
이제 CU 가 어떻게 작용하는 지 다음과 같이 살펴볼 수 있다. 먼저 두 큐비트 시스템의 기저 벡터는 |00〉, |01〉, |10〉, |11〉 순으로 쓸 수 있다. 제어 큐비트는 큐비트 0 이라 가정하자. 키스킷 표기에 따르면 텐서곱 연산의 오른쪽에 해당한다. 만약 제어 큐비트가 |1〉 이면, U가 작용할 때 기저 벡터들은 다음과 같이 변환된다.
CU 를 행렬로 나타내면 다음과 같다.
이러한 행렬 성분을 알아내려면, CU의 작용을 먼저 계산하고 내적을 계산한다.
다음 예제에서 볼 수 있듯이, 이 연산은 키스킷에서 cu(q[0], q[1])로 구현되어 있다. 만약 큐비트1 이 제어 큐비트이고 큐비트0이 표적(target) 큐비트라면, 기저 벡터는 다음과 같이 변환된다.
이는 CU의 행렬 형태가 다음과 같음을 의미한다.
3.3.2.1. 제어 파울리 게이트들
3.3.2.1.1. 제어 반전 게이트(또는 제어 X 게이트 또는 제어 NOT 게이트)
제어 반전 게이트는 제어 큐비트의 상태가 |1〉일 때 표적 큐비트를 반전시킨다. 만약 cx(q[1], q[0])와 같이 제어 큐비트가 MSB 라면 그 행렬은 다음과 같다
반대로, cx(q[0], q[1])과 같이 제어 큐비트가 LSB이면 이 게이트는 다음 행렬과 동일하다.
회로의 구현은 다음과 같다.
코드 229번 라인의 출력은 다음과 같다. (컴포저에서 CX게이트는 ⊗가 아니라 ⊕임에 유의하자.)
코드 232번 라인의 출력은 다음과 같다. 제어 큐비트가 |0〉이므로, 표적 큐비트에 영향이 없다.
코드 234번 라인의 출력은 다음과 같다.
[[1.+0.j 0.+0.j 0.+0.j 0.+0.j]
코드 226번 라인의 주석을 풀어서, 제어 게이트를 |1〉 로 반전시키면, 코드 232번 라인의 상태 벡터는 다음과 같이 블로흐 구에 도식된다.
3.3.2.1.2. 제어 Y 게이트
제어 큐비트가 MSB이면, Y 게이트를 목표 큐비트에 적용한다. 이 때의 행렬식은 다음과 같다.
반대로, 제어 큐비트가 LSB이면 다음의 행렬식이 적용된다.
회로의 구현은 다음과 같다.
코드 242번 라인의 출력은 다음과 같다.
코드 245번 라인의 출력은 다음과 같다.
코드 248번 라인의 출력은 다음과 같다.
코드 239번 라인의 주석을 제거하면 코드 245번의 출력이 다음과 같이 바뀐다.
3.3.2.1.3. 위상 제어 게이트(또는 제어 Z 게이트 또는 위상 반전 게이트)
위상 반전 게이트는 제어 큐비트의 상태가 |1〉 일 때 표적 큐비트의 위상을 뒤집는다. 제어 큐비트가 MSB인 경우나 LSB인 경우에 상관없이 행렬은 같은 모양이다.
회로의 구현은 다음과 같다.
코드 255번 라인의 출력은 다음과 같다.
코드 258번 라인의 출력은 다음과 같다.
코드 261번 라인의 출력은 다음과 같다.
코드 252번 라인에서 주석을 제거하면 코드 258번의 출력은 다음과 같다.
3.3.2.2. 제어 하다마드 게이트(Controlled hadamard gate)
제어 큐비트가 |1〉이면 하다마드 게이트를 표적 큐비트에 적용한다. 다음 행렬은 제어 큐비트가 LSB인 경우이다.
이 회로의 구현은 다음과 같다.
코드 267번 라인의 출력은 다음과 같다.
코드 270번 라인의 출력은 다음과 같다.
코드 273번 라인의 출력은 다음과 같다.
제어 큐비트인 q[0]가 0이므로, 표적 큐비트[1]의 상태가 바뀌지 않는다. 코드 264번의 주석을 해제하여 제어 큐비트를 X게이트로 반전시키면, 다음의 상태 벡터를 볼 수 있다.
3.3.2.3. 제어 회전 게이트들(Controlled rotation gates)
3.3.2.3.1. Z 축을 기준으로 한 회전 제어 게이트(Controlled rotation around z-axis)
LSB의 제어 큐비트가 |1〉이면, 표적 큐비트를 Z축을 중심으로 회전시킨다. 행렬식은 다음과 같다.
양자 회로의 구현은 다음과 같다.
코드 283번 라인의 출력은 다음과 같다.
코드 286번 라인의 출력은 다음과 같다.
코드 289번 라인의 출력은 다음과 같다.
코드 280번 라인의 주석을 제거하면 코드 286번 라인의 블로흐 구가 다음과 같이 출력된다.
3.3.2.3.2. 제어 위상 회전 게이트(Controlled phase rotation)
두 큐비트가 모두 |11〉 상태에 있으면 위상 회전을 수행한다. 이 경우 제어 큐비트가 MSB나 LSB에 상관없이 다음의 행렬이 적용된다.
키스킷을 이용한 양자 회로의 구현은 다음과 같다.
코드 289번 라인의 출력은 다음과 같다.
코드 301번 라인의 출력은 다음과 같다.
코드 304번 라인의 출력은 다음과 같다.
코드 294번 라인의 주석을 해제하면, 코드 301번 라인의 출력은 다음과 같다.
3.3.2.3.3. 제어 u3 회전 게이트
제어 큐비트(코드에서는 LSB)의 상태가 1〉이면 표적 큐비트에 u3 회전을 수행한다. 행렬식은 다음과 같다.
양자 회로의 구현은 다음과 같다.
코드 312번 라인의 출력은 다음과 같다.
코드 315번 라인의 출력은 다음과 같다.
코드 318번 라인의 출력은 다음과 같다.
코드 309번 라인의 주석을 제거하면 코드 315번 라인의 출력은 다음과 같다.
3.3.2.4. 교환 게이트(Swap gate)
교환 게이트는 두 큐비트의 상태를 서로 바꾼다. 이는 기저 벡터를 다음과 같이 변환한다.
|00〉 → |00〉, |01〉 → |10〉, |10〉 → |01〉, |11〉 → |11〉
행렬식은 다음과 같다.
구현은 다음과 같다.
코드 326번 라인의 출력은 다음과 같다.
코드 329번 라인의 출력은 다음과 같다.
코드 332번 라인의 출력은 다음과 같다.
코드 323번 라인의 주석처리를 제거하면 코드 329번 라인의 출력은 다음과 같다.
3.3.3. 삼중 큐비트 게이트
널리 사용되는 두 가지 삼중 큐비트 게이트가 있다. 세 큐비트의 경우 기저 벡터는 다음과 같이 정렬된다.
|000〉, |001〉, |010〉, |011〉, |100〉, |101〉, |110〉, |111〉
비트열처럼 정수 0, 1, 2, ..., 7 을 나타낸다. 키스킷은 첫번째 큐비트를 가장 오른쪽에, 세번째 큐비트를 가장 왼쪽에 위치하는 표현을 사용함을 재차 강조한다.
3.3.3.1. 토폴리 게이트
토폴리 게이트는 LSB로 첫번째와 두번째 큐비트가 모두 |1〉일 때 세번째 큐비트를 플립한다. 즉, 두 개의 제어 큐비트가 모두 |1〉인 경우 표적 큐비트를 플립한다.
행렬식으로 표현하면 다음과 같다.
회로의 구현은 다음과 같다.
코드 345번 라인의 출력은 다음과 같다.
코드 348번 라인의 출력은 다음과 같다.
코드 351번 라인의 출력은 다음과 같다.
[[1.-0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j]
[0.+0.j 1.-0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j]
[0.+0.j 0.+0.j 1.-0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j]
[0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 1.-0.j]
[0.+0.j 0.+0.j 0.+0.j 0.+0.j 1.-0.j 0.+0.j 0.+0.j 0.+0.j]
[0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 1.-0.j 0.+0.j 0.+0.j]
[0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 1.-0.j 0.+0.j]
[0.+0.j 0.+0.j 0.+0.j 1.-0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j]]
코드 341 ~ 342번 라인의 주석 처리를 해제하면, 코드 348번 라인의 출력은 다음과 같다.
3.3.3.2. 제어 교환 게이트(또는 프레드킨 게이트)(Controlled swap gate, or Fredkin gate)
첫번째(LSB) 큐비트가 |1〉일 때 두번째와 세번째 큐비트를 교환한다. 즉, 제어 큐비트가 |1〉이면, 두 표적 큐비트를 교환한다. 수식은 다음과 같다.
프레드킨 게이트를 행렬로 표현하면 다음과 같다.
키스킷을 이용한 양자회로 구현은 다음과 같다.
코드 361번 라인의 출력은 다음과 같다.
코드 364번 라인의 출력은 다음과 같다.
코드 367번 라인의 출력은 다음과 같다.
코드 357~358번 라인의 주석처리를 제거하면 코드 364번 라인의 출력은 다음과 같다.
3.4. 비 유니타리 연산들(Non-unitary operations)
양자 회로에서 사용 가능한 모든 유니타리 연산들을 살펴보았으니, 이제 유니타리가 아닌 연산들을 살펴보자. 유니타리가 아닌 연산에는 측정, 큐비트의 초기화(reset), 전통적인 조건 연산이 있다.
3.4.1. 측정
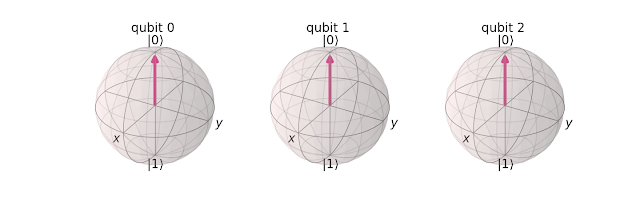
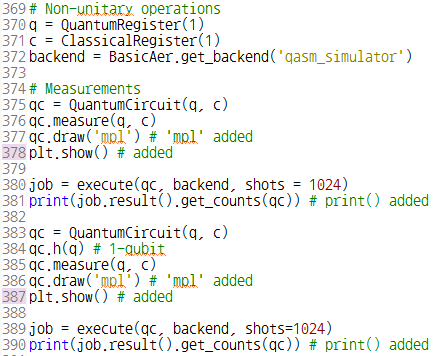
양자 컴퓨터에서 측정을 수행해도 모든 정보를 얻을 수는 없다. 양자 상태는 표준 기저에 사영된다. 아래 두 예는 각각 양자 상태들이 기저 상태 중 하나로 준비되거나 중첩 상태로 준비되는 회로를 보여준다.
코드 378번 라인의 출력은 다음과 같다.
코드 381번 라인의 출력은 다음과 같다. 1024회 shot 모두 '0'으로 측정되었다.
{'0': 1024}
코드 387번 라인의 출력은 다음과 같다.
코드 390번 라인의 출력은 다음과 유사하게 약 50%는 0, 나머지 약 50%는 1로 측정되었다.
{'0': 513, '1': 511}
3.4.2. 재설정(reset)
계산 중에 큐비트들을 |0〉 상태로 재설정하는 것도 가능하다. 재설정은 가역 연산이 아니므로 게이트 연산이 아님을 주목하자. 키스킷 구현은 다음과 같다.
코드 398번 라인의 출력은 다음과 같다.
코드 401번 라인의 출력은 다음과 같다.
{'0': 1024}
코드 408번 라인의 출력은 다음과 같다.
코드 411번 라인의 출력은 다음과 같다. 두 회로 모두 100% 로 결과값이 0 상태임을 알 수 있다.
{'0': 1024}
3.4.3. 조건 연산자
전통적인 레지스터의 상태를 조건으로 연산하는 것도 가능하다. 구현은 다음과 같다.
코드 420번 라인의 출력은 다음과 같다.
코드 423번 라인의 출력은 다음과 같다.
{'1': 1024}
코드 417번 라인에서, 전통적인 레지스터의 초기값은 0이므로, 양자 레지스터 q[0]에 플립이 발생한다. 양자 레지스터의 초기값도 0이므로, X 게이트 플립이 100% 발생하여 1로 측정된다.
코드 431번 라인의 출력은 다음과 같다.
코드 434번 라인의 출력은 하다마드 게이트에 의해 큐비트 q3는 0과 1이 각각 약 50%의 확률을 갖는다. 코드 437번 측정에서 q3가 1인 경우, 전통적인 레지스터 c0는 측정에 따라 1이고 428번 라인의 조건(0일 때 적용)에 따라 X게이트를 적용하지 않아서 코드 434번의 결과는 q3가 1이다. 반대로, 코드 437번 측정에서 q3가 0인 경우, 전통적인 레지스터 c0도 0이고 428번 라인의 조건(0일 때 반전)이 적용되어 X 게이트로 q3가 반전된다. 따라서 q3 측정 결과는 역시 1이다. 따라서 코드 434번의 결과는 다음과 같다.
{'1': 1024}
전통적인 레지스터 c의 값은 초기에 0이므로, 417번 라인에서 x 게이트 플립이 양자 레지스터 q[0]에 적용된다. 따라서
3.5. 임의 초기화
큐비트 레지스터를 임의의 상태로 초기화할 수 있다. n큐비트의 임의의 상태는 각 진폭의 절대값의 제곱을 모두 더했을 때 1이 되는 2ⁿ 개의 진폭을 나타내는 숫자로 구성된 벡터로 표현할 수 있다. 예를 들어, 다음의 세 큐비트 상태를 준비하자.
위 상태를 구현하면 다음과 같다.
코드 455번 라인의 출력은 다음과 같다.
코드 460번 라인의 출력은 다음과 같다.
충실도(Fidelity)는 두 상태가 같은지 확인하는데 유용하다. 두 순수한 양자 상태의 충실도는 다음과 같이 구한다.
F(|ψ₁〉, |ψ₂〉) = |〈ψ₁ | ψ₂〉|²
충실도는 오직 두 큐비트가 동일한 경우에만 1이다. 코트 463번 라인의 출력은 다음과 같다.
1.0000000000000004
3.5.1. 세부 내용
원하는 상태를 준비하는 다양한 방법들이 있지만, 키스킷에서는 Shende 등이 제안한 방법[4]을 사용한다. 이 논문의 아이디어는 양자 레지스터가 애초에 원하는 상태로 시작했다고 가정한 다음 |00...0〉 상태로 변환하는 회로를 구성하는 것이다. 그리고 이 회로의 역변환을 구하여 초기화 회로를 얻는다.
임의의 양자 상태를 계산 가능한 기저(computational basis)의 영 상태(zero state)로 만들고자 큐비트의 얽힘을 푸는 과정을 반복한다. 임의의 단일 큐비트 상태 |ρ〉 는 Z축을 중심으로 회전하는 Φ-회전과 Y축을 중심으로 회전하는 θ-회전을 연이어 수행하여 상태 |0〉로 변환할 수 있다.
Ry(-θ)Rz(-Φ)|ρ〉 = reit|0>
지금 다루는 큐비트는 한 개가 아닌 n 개 이므로, 상태 벡터에서 가장 덜 중요한 비트(LSB)를 분리해 내고자 다음과 같이 성분 별로 묶어 분해한다.
이제 각 단일 큐비트 상태 |ρ0〉, ..., |ρ2n-1-1〉 은 적절한 각도 Φ와 θ를 찾아 |0〉으로 변환할 수 있다. LSB의 얽힘을 풀어나가는 이 과정을 모든 상태에 동시에 수행하는 유니타리는 다음과 같다.
따라서,
U는 블록 대각 행렬이므로, 양자 멀티플렉서(quantum multiplexor) 게이트로 구현할 수 있다. 양자 멀티플렉서에서 크기가 2ⁿ x 2ⁿ 이고, 2s 개의 블록 행렬로 구성된 블록 대각 행렬은 선택 큐비트(select qubit)가 s 개, 데이터 큐비트가 n - s개로 구성된 멀티플렉서와 동일하다. 이 때 선택 큐비트의 상태에 따라 데이터 큐비트에 적용되는 블록이 선택된다. 이러한 종류의 멀티플렉서는 기본 게이트 cr, rz 그리고 ry를 이용하여 재귀적으로 분해한 형태로 구현할 수 있다.
[1] 원문:
https://qiskit.org/documentation/tutorials/circuits/3_summary_of_quantum_operations.html
[2] 내 코드:
https://github.com/sungmin-net/python-qiskit-tutorials/blob/main/tutorial03_QuantumOperations.py
[3] 위키백과, '켤례전치': https://ko.wikipedia.org/wiki/켤레전치
[4] Vivek V. Shende 등, "Synthesis of Quantum Logic Circuits", https://arxiv.org/abs/quant-ph/0406176









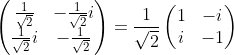




















































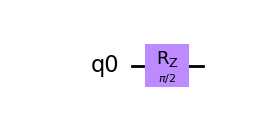









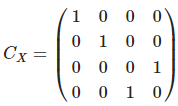






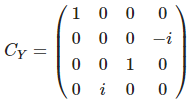









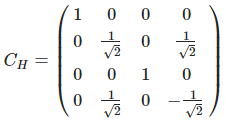




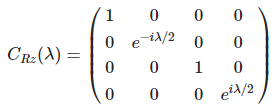









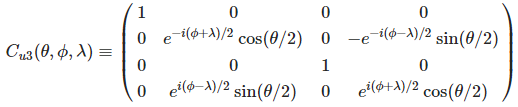


































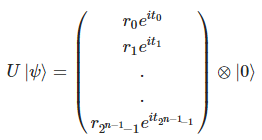
댓글 없음:
댓글 쓰기