이 글은 2020년 IEEE ICCCA 에서 공개된 Vaishali Bhatia 씨 등의 "An Efficient Quantum Computing technique for cracking RSA using Shor’s Algorithm" 논문[1]을 번역한 글입니다. 번역기를 사용하지 않으므로, 제 이해와 필요에 따라 원문과 차이가 날 수 있습니다. 논문에 포함된 표와 그림은 재도식하거나 생략합니다.
ABSTRACT
양자 컴퓨팅은 계산을 빠르게 수행할 수 있는 유망한 단어이다. 양자 컴퓨팅을 사용하는 동기는 전통적인 컴퓨터로는 어려웠던 많은 문제들을 빠르게 해결할 수 있다는 것이다. 전통적인 방법은 0과 1로 구성된 비트를 사용하는 반면 양자 컴퓨팅은 큐비트로 동작한다. 전통적인 컴퓨터는 계산이 병렬적으로 수행되더라도 저장 공간과 계산에서 중요한 문제를 갖는다. 양자 병렬성의 개념은 전통적인 컴퓨터와 비교하여 기하급수적으로 짧은(low time) 시간에 계산이 수행될 수 있도록 한다. 이 논문은 양자 컴퓨팅 알고리즘과, 어떻게 쇼어 알고리즘이 RSA 알고리즘을 깨뜨릴 수 있는 지에 대해 논한다. 큐비트의 얽힘과 중첩은 빠른 계산을 돕는다. 적용 가능성의 시현은 계산 시간, 저장 공간, 정확도, 기밀성, 효율성, 무결성과 가용성을 기반으로 평가되었다. 다양한 알고리즘 중 쇼어의 기법은 전통적인 계산 방식보다 더 우월하게 다양한 암호 알고리즘을 깨뜨릴 수 있다. 간단히 말해서, 논문은 다양한 양자 알고리즘에 대해 논의하고, 어떻게 쇼어 알고리즘이 RSA을 깨뜨릴 수 있는 지를 설명한다.
Ⅰ. INTRODUCTION
양자 컴퓨팅은 1980년대에 시작되었으며, 얽힘과 중첩 같은 기법과 함께 양자 역학 현상을 기반으로 한다. 컴퓨터를 사용하여 수행하는 계산을 양자 컴퓨터로 수행한 것은 1994년에 존재한 것으로 알려져 있다. 양자 컴퓨팅에 의해 해결된 첫 번째 문제는 16큐비트를 사용하여 해결된 스도쿠 게임이었다. 전통적인 컴퓨터 시스템에서는 0과 1의 두 가지 가능한 상태가 있지만, 양자 컴퓨팅은 각 비트가 두 가지 가능한 상태로 구성된 큐비트로 이루어진다. 2018년에 가능한 가장 큰 양자 컴퓨터는 72큐비트로 구성된다.
양자 컴퓨팅의 발전을 이끄는 아이디어는 사용자가 가용한 많은 양의 데이터를 처리할 때 계산 속도를 높이기 위한 병렬화 작업이 많은 수의 코어에서도 계산 시간이 길다는 점이다. 양자 컴퓨팅의 얽힘, 간섭, 중첩의 원리를 사용하면 대량의 데이터를 병렬로 처리하고 실행할 수 있다. 이 장점은 동적인 문제를 처리하는 데 도움이 될 뿐만 아니라 매우 빠른 시간 안에 어렵고 복잡한 문제의 해결책을 제공한다.
양자 역학에 깊이 들어가는 동안에 명확히 해야하는 기본 용어들이 있다. 원자나 입자가 자기장에 들어갈 때마다 위쪽 또는 아래쪽으로 편향되는 것을 스핀이라고 한다. 그림 1은 상하 운동으로 구성된 양자 컴퓨터의 스핀 운동을 보이는 반면, 전통적인 컴퓨터의 경우에는 상하좌우로 구성된다. 그러면 전통적적인 컴퓨터가 더 경우의 수가 많은 건가....
|+> = |0> + |1> / 2
|-> = |0> - |1> / 2
양자 컴퓨팅 분야의 다음 관련 용어는 양자 게이트이다. 전통적인 컴퓨터가 연산에서 AND, OR, NOR과 같은 논리 게이트를 사용하는 것과 유사하게 양자 컴퓨터는 연산을 수행하기 위해 파울리(Pauli)-X, 파울리-Y, 파울리-Z, 하다마드 게이트 등을 사용한다. 다음 연산은 0과 1의 중첩에 적용될 수 있는 하다마드 행렬을 나타낸다.
파장의 간섭은 원하는 결과를 얻기 위한 규비트 중첩의 부차적인 결과에 의해 수행된다.
얽힘은 둘 이상의 상태의 상관관계 또는 다른 상태에 대한 참조로 알려진 과정이다. 전통적인 컴퓨터의 경우 입자 간의 상관관계를 찾기가 매우 어렵기 때문에 가장 유망하게(prominent) 여겨진다.
그림3은 1970년대에 시작된 양자 컴퓨팅의 발전을 도식하며 현재까지 상업적 붐으로 확장되었다.
이 논문은 단원 1에서 양자 컴퓨팅 소개와 위에서 논의된 다양한 용어에 대한 세부 정보가 포함되고, 단원 2는 양자 컴퓨팅의 다양한 알고리즘으로 구성되며, 단원 3은 이 분야의 다양한 연구자들이 수행한 작업을 보여주는 문헌 조사를 다루고, 단원 4는 쇼어 알고리즘이 RSA 알고리즘을 해독할 수 있는 방법을 보여주는 제안된 작업으로 구성되며, 단원 5는 결과 및 토론으로 구성되는 다양한 단원으로 나뉜다.
Ⅱ. QUANTUM ALGORITHMS
이 단원에서는 다양한 양자 알고리즘과 그 중요성에 대해 설명한다.
A. 도이치-조사 알고리즘(Deutsch-Jozsa algorithm)
이 알고리즘은 고전 컴퓨터와 경쟁하기 위해 1992년에 개발된 최초의 알고리즘이다. 입력을 0 또는 1로 취하고, 출력을 0 또는 1로 제공한다.
f : {0, 1} → {0, 1}
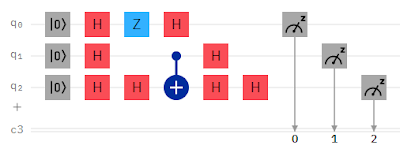
이 알고리즘은 출력으로 동일한 수의 0과 1을 가지고 있으면 균형을 이룬다고 한다. N 자리 이진수를 입력으로 취하며, 결과를 0 또는 1로 제공한다. 최악의 경우 2n-1 + 1 의 시간 복잡도를 가진 전통적인 컴퓨팅에 비해 기하급수적으로 낮은 복잡도로 어려운 문제를 해결할 수 있었다. 입력에 하다마드 연산을 적용하고, 오라클 함수를 적용하기 위한 모든 구성을 준비한 다음 매핑과 함께 그룹화를 적용하여 결과를 0 또는 1로 제공하는 원리를 기반으로 동작한다. 오라클 함수는 f(x) = 0 인 경우 I-게이트를 적용하고, f(x) = 1 인 경우 X-게이트를 적용한다. 그림3은 입력 n = 3 비트 값에 대해 Qiskit 을 사용하여 구현한 도이치-조사 알고리즘의 구현을 보여준다. Qiskit 이 아니고 IBM 양자 컴포저입니다만...
B. 그로버 알고리즘(Grover's algorithm)
그로버 알고리즘은 1996년에 개발되었으며, 기존의 O(N)과 비교하여 O(√N)의 복잡도(complexity)를 가지는 병렬성의 원리를 기반으로 동작한다. 기본적으로 데이터베이스 검색에 사용되고, 비구조적 데이터에도 주로 동작한다. 예를 들어, 우리가 n 개의 아이템을 가지고 있고, 어떤 아이템을 찾아야 할 때 이 알고리즘이 사용될 수 있다.
f(x) : {0 for u = x and 1 for u != x}
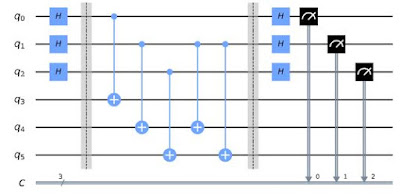
그림 5는 입력 n = 4비트 인 그로버 알고리즘의 구현을 보여준다.
C. 사이먼 알고리즘(Simon's algorithm)
이 알고리즘은 1997년에 소개되었으며, 이 경우 양자 이산 푸리에 변환(Quantum discrete fourier transformation)으로 알려져 있는 이산 푸리에 변환을 기반으로 한다. 하나의 입력이 하나의 출력 또는 두개의 입력이 하나의 출력으로 구성되는 일대일 또는 이대일 매핑 방법에서 동작한다. 그림 6은 사이먼 알고리즘의 구현을 보여준다.
D. 쇼어 알고리즘(Shor's algorithm)
쇼어 알고리즘은 1994년 피터 쇼어에 의해 개발되었으며, 양자 컴퓨터를 사용하여 다항 시간에 알고리즘의 소인수를 찾는 작업이다. 우리가 쇼어 알고리즘을 통해 소인수를 찾으려고 할 때 쇼어 알고리즘은 쇼어의 소인수 분해 알고리즘으로도 알려진다. 큰 수들의 소인수들은 매우 계산하기 어렵다는 개념을 기초로 하며, 객체의 주기성을 측정하는 기법을 사용한다.
큰 수의 소인수를 찾는 문제는 전통적인 컴퓨터에게 어려운 문제로 여겨진다. p 와 q 가 큰 수이고, N = p * q 인 N이 알려진 경우에 p 와 q 를 찾는 작업을 가정한다. Brute force 방법으로 찾을 수 있겠지만, 얼마나 많은 시간이 걸릴지는 알 수 없다. 전통적인 컴퓨터에서는 Brute force 방법보다 더 나은 다른 알고리즘이 없다. 쇼어 알고리즘은 소인수 분해 기법으로 주기 함수(periodic function)의 주기(period)를 찾는 작업을 목적으로 한다.
쇼어 알고리즘에 사용되는 연산자는 양자 푸리에 변환이다. 이는 소인수 분해 알고리즘과 함께 잘 동작하고, 현재까지 21큐비트의 소인수를 찾을 수 있다. 구현을 위한 단계로 우선 레지스터들이 텐서 곱을 통해 Q 상태의 중첩으로 초기화된다. 이 상태를 사용하여 양자 함수 f(x)가 입력 레지스터들에 생성되어 역 양자 푸리에 변환(Inverse Quantum Fourier Transformation)이 적용된다. 그 다음 다른 축소 불가능한 작업이 수행된다. 이 작업들은 소인수 분해 문제를 축소하는 작업을 주로 수행한다.
그림 7은 쇼어 알고리즘이 어떻게 동작하는 지를 보여주는 흐름 순서도를 나타낸다.
Ⅲ. RELATED WORK (생략)
Ⅳ. METHODOLOGY
RSA 는 공개키와 개인키 두 개의 키를 사용하는 개념의 효율적인 알고리즘으로 하나의 키는 암호화에 사용되고 다른 키는 복호화 과정에 사용된다. 사용자는 키가 안전할 때까지 안전하다.
이 알고리즘은 메시지의 크기가 작으면 깨뜨리기가 쉬운 반면에 비트의 수가 증가하면 깨뜨리기가 더 어렵다. 전통적인 컴퓨터가 계산하기 매우 어려웠던 문제들을 쉽게 다룰 수 있는 쇼어 알고리즘이 1994년에 많은 비트를 가진 소인수 분해 문제를 다룰 수 있게 되었다. 두 소수의 소인수를 찾는 일은 전통적인 컴퓨터에게는 어렵지만 양자 컴퓨터에서는 쉽게 다룰 수 있다.
RSA 알고리즘에서 사용되는 공개키는 소인수를 기반으로 하며, 암호화 과정에서 사용된다. 만약 소인수들이 알려지지 않으면 이 수들을 복호화하기 어려운 것으로 알려져 있다. 큰 수의 소인수를 찾는 문제의 복잡도는 기하급수적으로 크다. [6] 다항식의 인자를 찾는 문제의 복잡도는 고전 컴퓨터의 경우 O(exp(3√64/9n(logn)^2)) 이고, 양자 컴퓨터의 경우 O(n3 log n)이다.
21의 최대공약수를 찾는 개념을 설명하는 예를 들어보자. 그리고 우리는 GCD(21, 15)에서,
- 21 = 1 x 15 + 6
- 15 = 2 x 6 + 3
- 6 = 2 x 3 + 0
따라서 3은 두 수의 공통이므로, 이것이 21과 15의 최대 공약수이다. 이제 공식 xn mod N 을 사용해보자. 여기에서 x 의 값은 반복되기 시작하면 중지한다. 이 예제를 설명하면,
- 20mod 15 = 1 mod 15
- 21mod 15 = 2 mod 15
- 22mod 15 = 4 mod 15
- 23mod 15 = 8 mod 15
- 24mod 15 = 1 mod 15
위 식에서 값 4부터 반복되므로, 주기값 r 은 4가 된다. 주기값이 짝수인 경우에는 연산이 가능하지만, 홀수인 경우에는 다른 값을 추측한다.
이 기법에서 우리는 x 값을 추측하는 것으로 시작하였고 가장 큰 어려움은 주기값을 찾는 일이다. 쇼어 알고리즘은 BPP(Bounded-error probabilistic polynomial time, 유계오차 확률적 다항시간[7])의 개념을 기반으로 하여, O(n)의 복잡도로 모든 문제를 해결할 수 있는 다항식 기술을 기반으로 한다.
양자컴퓨터를 사용하여 해결된 주요 문제는 주기값 찾기이다. 방정식의 주기를 계산하기 위해 유클리드 호제법(Euclid Algorithm)을 사용하여 값을 구한다. 우리의 예제에서 주기값은 4 였고, N 은 15였으므로,
gcd(15, 4+1) = gcd(15, 5) = 5
gcd(15, 4-1) = gcd(15, 3) = 3
위 두개의 식을 통해서 우리는 N 이었는 15가 5 x 3 이라는 것을 구하였다.
Ⅴ. RESULTS AND DISCUSSIONS
결과적으로, 실행 시간과 비트의 수에 관련된 다양한 모델이 있으며, qiskit 을 이용한 도식 결과는 다음 그림과 같다.
[3] 논문의 그림과 IBM의 그림이 상이하여 IBM의 그림을 참고하여 도식하였다. 자세한 설명은 다음 링크 참고.
https://quantum-computing.ibm.com/docs/iqx/guide/deutsch-jozsa-algorithm
[6] RSA에 대한 설명은 나무위키가 가장 뛰어나다고 생각한다. 링크는 아래
https://namu.wiki/w/RSA 암호화







댓글 없음:
댓글 쓰기