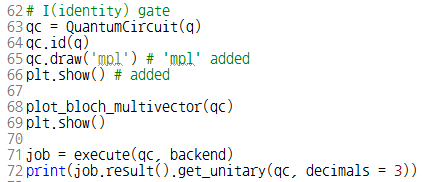
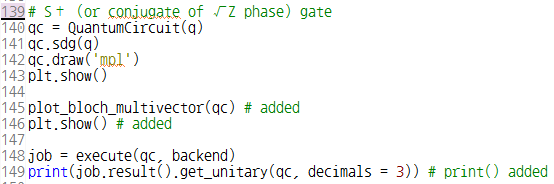
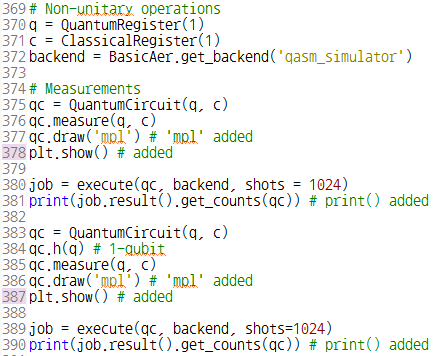
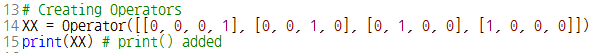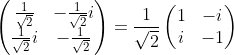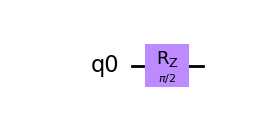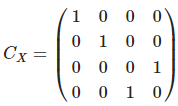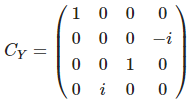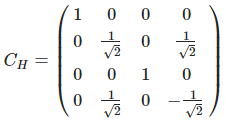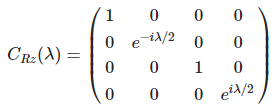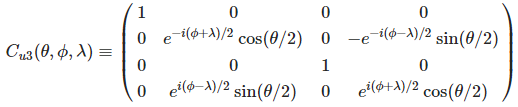이 글은 제가 IEEE SecDev 2021 [1] 에 투고하여 게재된 글입니다. 논문의 Footnote 와 Reference 는 하나로 통합합니다.
Abstract
Remote unlocking for Android devices may benefit both users and manufacturers. Users can continue using the device without factory-resetting when they unexpectedly forget their passphrases. Manufacturers can improve non-face-to-face customer services in the COVID-19 era. Nevertheless, not many manufacturers support remote unlocking services for Android devices. If the remote unlocking service is triggered by requests over-the-air, it may increase the attack surface of Android security. Android security is hardware-based (e.g., hardware-backed Keystore), so we seek to preserve this security level by designing a new remote unlocking service without modifying trusted execution environments. Our design supports two-factor authentication, distributed authority, trust-boundary minimization, and key management. Since a synthetic password used for remote unlocking is not exposed to the outside of an Android device, the manufacturer still cannot unlock the device without user consent. We identify 208 security threats in the proposed remote unlocking service using the STRIDE model and ensure that our design has countermeasures for all high-level security threats. After passing quality verification and penetration tests, the proposed remote unlocking service has been officially installed on commercial devices.
Ⅰ. Introduction
An Android remote unlocking service allows its user to unlock an Android device through the Internet [2]. Once a user registers a passphrase such as a PIN, pattern, or password with an Android device, a screen lock is set. If supported, the user can also activate the remote unlocking service for her device. After this, when the user cannot unlock the device (say, forgetting her passphrase), the user can visit the remote unlocking service website and make the device unlocked via the Internet. The device receives a secure message over the Internet and can be unlocked.
Not many manufacturers support such a service due to the difficulty of designing and implementing a secure remote unlocking service. From the perspective of security, the remote unlocking service can be risky since it inevitably increases the attack surface. Because, unlike conventional offline device unlocking, this service allows device unlocking through the Internet. Thus, if the remote unlocking service is not carefully designed, the device might be unlocked by a malicious attacker and its user's personal data might leak.
However, from the perspective of usability, the remote unlocking service benefits both users and device manufacturers. If the device users accidentally forget the passphrase of the screen lock, the remote unlocking service provides users with an alternative method of unlocking their device. In this way, the device can be reused without performing factory-resetting. In contrast, an Android device that does not support the remote unlocking service needs factory-resetting to be reused if the device cannot be unlocked. [3] Due to the unwanted factory-resetting, users lose valuable data such as photos, contacts, and text messages that have not been backed up. Briefly, since the remote unlocking service allows users to unlock their devices without going through factory-resetting, the users can avoid this data loss.
Remotely unlocking devices also helps increase the manufacturer's profit. The manufacturers can improve customer services by supporting remote unlocking services. Also, since non-face-to-face services reduce customer visits to the service center, the manufacturers can save their customer service costs. Especially in the COVID-19 era, adopting non-face-to-face services is highly encouraged.
For the devices with Android 10 or higher, file-based encryption (FBE) is essential to obtain Google mobile service (GMS) certificates [4]. Once FBE is applied to an Android device, the master key that encrypts the device is derived from the user's passphrase. Thus, even its manufacturer, who has the system permission authority, cannot obtain the information about the encryption key. It means that it is hard for the manufacturer to overhaul the locked device. Assume that there is an Android device that cannot be unlocked. If the user claims that the correct passphrase cannot unlock the device, the manufacturer must struggle to determine whether the user typed an incorrect passphrase or the device is defective. In general, any software and hardware have the possibility of malfunctioning. Moreover, the Android user authentication consists of various modules such as Keyguard, Lockscreen, Gatekeeper, LocksettingService, Keymaster, and Keystore. Thoughtful manufacturers conduct comprehensive testing before launching their devices, but testing all use-cases is impossible. If the device supports the remote unlocking service and the user enabled the service, the manufacturer can help the user unlock her device. Then, under the user agreement, the manufacturer can examine the locked device to find which module went wrong.
The advantages and challenges of the remote unlocking service are evident. While this service benefits both users and manufacturers, it also increases the attack surface. Thus we seek to develop a new remote unlocking service that preserves the security level of Android. The proposed remote unlocking service utilizes a synthetic password (SP). Therefore, it preserves the hardware-backed security level, but it requires no modifications to the Android hardware security. To the best of our knowledge, the proposed remote unlocking service is the first case to leverage the SP for personal users, not for enterprises.
We adopt the STRIDE model [5] to identify the threats and add the corresponding countermeasures in security design. Finally, the proposed solution has been installed onto commercial devices after passing quality verification by a manufacturer and penetration tests by a third party.
The rest of this paper consists of the following. Section Ⅱ briefly describes the current Android security features. Section Ⅲ addresses our security design. Section Ⅳ explains our security design from an implementation perspective. Section Ⅴ analyzes security threats and describes their countermeasures. Section Ⅵ compares our research with other works. In Section Ⅶ, we share the conclusions.
Ⅱ. Background
Android provides various security features, which are leveraged to design the proposed remote unlocking service.
A. Synthetic Password
User authentication in modern Android devices is based on hardware security [5]. User passphrases are encrypted and stored in the device's hardware-backed Keystore and not exposed outside the device. For personal Android devices, a device user is the same as its owner. However, in enterprise scenarios, a device user and an owner may be different [6]. In the enterprise scenario, the device owner should be able to reset the passphrase set by the previous user so that other users can reuse the device. For this, Android introduces a security primitive, the SP, starting from its version 8 (or Oreo). The DevicePolicyManager (DPM) in the Android framework provides application programming interfaces (APIs) that only the device owner (specifically, the organization's IT administrator) can activate and use the SP to unlock the device with a reset password token (RPTkn) [7][8].
B. Android Application Sandbox
The Android platform uses Linux user-based protection to identify and isolate an app's resources [9]. The user ID (UID) that Android assigns to each app provides a kernel-level app sandbox, and each app runs in the sandbox. Thus, Android apps cannot communicate directly with each other by default. Instead, only limited access through the OS is allowed. Also, since the app sandbox is inside the kernel, this security mechanism protects all modules above the kernel. To break the sandbox, the Linux kernel must be compromised. However, as Android has been upgraded, various access controls such as SELinux and kernel protection schemes have been applied [9].
C. Android Application Integrity
All apps running on the Android platform must be signed by their developers [10]. Also, legitimately signed apps normally run with different UIDs. However, if an app wishes to share the same sandbox with other apps at runtime, these apps must be signed with the same key. The apps signed with the same key can declare a shared UID in their Android manifest files. As the Android app signing scheme has been upgraded, the performance and security have been further enhanced [10].
D. Android Permissions
Android apps declare permissions in their manifest files to interact with other apps. Specific permissions are verified at the app's install time or execution time. Thus, they can be limited depending on the app's signature. Also, new permissions can be declared to restrict access from other apps [11].
Ⅲ. Security by Design
The security level of modern Android devices is deemed hardware-backed security [12][13]. This means that a user's keys are not exposed outside of its hardware security module (HSM). Thus, even the device manufacturer cannot arbitrarily unlock the device without the consent of the user.
A. Design Goals
In this section, we cover the security goals in the design of our remote unlocking service.
1) Preserving hardware-backed security: Security parameters used in remote unlocking must have a trust anchor that has its basis in the HSM. In a nutshell, a symmetric key for an AES cipher should not be exposed outside of the Android hardware Keystore, and the private key of an RSA cipher should not be disclosed outside of the HSM. See Section Ⅳ.A for details.
Even standard security measures would have vulnerability if poorly operated or unexpectedly misimplemented. Therefore, relying on a single security measure would not provide a sufficient security level. So, we intentionally overlap multiple security measures if the security enhancement is needed. See Section Ⅳ.F for details.
2) Two-factor authentication: In general, there are three types of authentication mechanisms, what-you-know, what-you-have, and what-you-are. A password represents what-you-know authentication. A credit card is an example of what-you-have. Biometric features such as fingerprint and iris are what-you-are authentication. We secure the proposed remote unlocking service by combining two of the three authentication techniques. First, requesting the user to enter her ID and password is the what-you-know authentication. Second, a mobile device itself can be the what-you-have authentication as only the user who possesses the device can trigger the remote unlocking service (say, selects a button in the device screen). Therefore, even the service providers [14] cannot unlock the device they do not have. See Figure Ⅰ and Section Ⅲ.C.2 for details.
3) Distributed authority: The unlocking server could be implemented as a single entity. However, to avoid the single point of compromise, our design divides the unlocking server into three entities: an account server, a database server, and a web interface server. That is, the compromise of a single server will not lead to unlocking an arbitrary device (Suppose that the attacker obtains an Android device of arbitrary victims.). See Figure Ⅱ and Section Ⅲ.C.2 for details.
4) Trust-boundary minimization: Besides third-party apps signed with the private keys of corresponding developers, an Android device has many system-privileged apps of different developers signed with the same platform key [15]. As the system-privileged apps can also call the SP-related APIs even if they are not related to the remote unlocking service, we need to add a new access control mechanism beyond the Android permission system. See Ⅳ.D for details.
5) Key management and compatibility: The server administrators should be able to change the public/private key pairs in their HSMs, e.g., due to key expiration or cipher change. Also, the proposed design should support forward compatibility by allowing the administrators to add new parameters related to the ciphers or expand the service functions. Meanwhile, it must consider backward compatibility for devices whose update support is expired. See Section Ⅳ.F for details.
B. Design Components
The structure of our service is shown in Figure Ⅰ. This section describes the major data elements and functional components of our service.
1) Reset password token (RPTkn): This is a 256-bit random value generated by an Android device that may have to be unlocked later. This is neither stored in the device storage nor left in the memory. Immediately after being generated, the RPTkn is encrypted with the hardware-backed AES key and then encrypted again with the RSA public key of the database server (DBS) by the remote unlocking app (RUApp). It will then be delivered to the DBS over TLS and zeroized in the device. When the device registration phase completes, the DBS stores the AES encrypted RPTkn. Thus, even the DBS cannot see the plaintext RPTkn.
2) User service account (USAcnt): This is the user's service account value saved in the device, for example, userid@manufacturer.com. To activate the remote unlocking service, the user saves her account in the AccountManager of the Android framework and agrees to the terms of the service. The service agreement includes that a network connection is enabled by RUApp when the remote unlocking service is triggered. Since the USAcnt is authenticated by a single entity, which is the account server, the same USAcnt is used in both the device and the web interface server (WIS). This data is encrypted with the RSA public key of the WIS by RUApp and decrypted in the WIS. Thus, the DBS cannot see the plaintext USAcnt.
3) Device Identifier (DevId): This data is an inherent value by which the service provider identifies a specific device. This is an international mobile equipment identity (IMEI) value for a device that can make a phone call, or a manufacturer serial number (MSN) value for a device that supports WiFi only. This is encrypted with the RSA public key of the DBS and transmitted to the DBS and WIS over TLS.
4) Remote unlocking app (RUApp): We develop this app from scratch for the remote unlocking service. Only this app can access new DPM APIs that control the SP in personal use scenarios (See Ⅳ.D). It also performs TLS connection setup with the DBS, payload encryption using an RSA cipher, payload signature / nonce / timestamp verification, RPTkn generation, AES encryption, and decryption of an RPTkn using the Android Keystore.
5) Database server (DBS): This server handles the communication with the device over TLS and stores the encrypted RPTkn of the device. The payload received from RUApp is decrypted using the DBS's RSA private key stored in its HSM. Also, the DBS delivers a part of the payload from RUApp to the WIS or the payload received from the WIS to RUApp.
6) Web interface server (WIS): We develop this server from scratch to handles the unlocking request from the user. The user visits the WIS and logs in using her USAcnt, which was saved on her device. When the device is waiting for remote unlocking, the user can select the device on the web page using another online machine.
C. Data Flow Diagrams (DFDs)
Our remote unlocking service has two phases: device registration and device unlocking. Each phase consists of the following interactions. See Section Ⅳ.F for details.
1) Device registration: Figure Ⅰ shows the DFD of the device registration phase. After the user sets her passphrase with LockSettingsApp, she can activate the remote unlocking service. As a precondition [16], (R1) LockSettingsApp calls AccountApp to set her USAcnt. (R2) The device user logs into her USAcnt via the Account server. (R3) If succeeded, the USAcnt is saved in AccountManager. (R4) The user activates the remote unlocking service. (R5) LockSettingsApp checks whether the user accepts the service agreement and (R6) requests RUApp to create an RPTkn. (R7) RUApp creates the RPTkn using remote unlocking APIs added to the DPM and performs AES encryption using the Keystore. (R8) RUApp returns only the pass/fail result of RPTkn creation to LockSettingsApp. (R9) LockSettingsApp calls KeyGuardApp to request the user to input the passphrase again. (R10) The user inputs the current passphrase [17]. (R11) LockSettingsApp requests RUApp to register the RPTkn with the DBS. (R12) RUApp gets the USAcnt through AccountManager and encrypts it with the RSA public key of the WIS. The RPTkn and DevId are encrypted with the RSA public key of the DBS. (R13) Then RUApp transmits the payload (see Figure Ⅲ) including the device's nonce (DevNonce) to the DBS through a TLS connection. (R14) The DBS decrypts the payload by using its HSM. (R15) The DBS sends the DevId and encrypted USAcnt to the WIS. (R16) The WIS uses its HSM to decrypt and store the USAcnt. (R17) The DBS sends the result (see Figure Ⅲ) of the device's remote unlocking service registration and its signature to RUApp. (R18) RUApp verifies the DBS's signature with the DevNonce and returns the result to LockSettingsApp. (R19) LockSettingsApp shows the result of the device registration to the user.
2) Device unlocking: Figure Ⅱ shows the DFD of unlocking the registered device. (U1) The user fails to unlock the device several times (say, forgets her passphrase). (U2) Keyguard checks the user consent to use the remote unlocking service through AccountApp and (U3) checks whether the remote unlocking service is activated through the DPM. If both conditions are satisfied, a throttling screen [18] displays a button to start the remote unlocking service. (U4) The user selects the button. (U5) KeyGuard calls RUApp. (U6) RUApp sends a payload (see Figure Ⅳ) including a fresh DevNonce to request (i) the RPTkn, and (ii) the WISSign (see Section Ⅳ.F.9) to the DBS through a TLS connection. (U7) The DBS requests a payload from the WIS. (U8) Using another machine, the user logs in to the WIS with her USAcnt. (U9) The WIS authenticates the user through the account server. (U10) The user selects the device currently waiting for remote unlocking. (U11) The WIS uses its HSM to sign her USAcnt with the WIS's timestamp (WISTimeStamp). (U12) The WIS sends the payload to the DBS securely. (U13) The DBS uses its HSM to complete the payload (see Figure Ⅳ). (U14) Then the DBS replies to the RUApp's request over the TLS connection. (U15) RUApp verifies the freshness of WISTimeStamp and the WIS signature with the USAcnt saved in AccountManager. Also, RUApp verifies the DevNonce and the DBS signature. (U16) If they are valid, RUApp decrypts the RPTkn and unlocks the device. If succeeded, the user can see the unlocked device. (U17) RUApp notifies the DBS of the device unlocking result over the TLS connection. (U18) The DBS notifies the WIS of the result. (U19) The user can also see the remote unlocking result from the WIS.
The device could send the data intended for the WIS directly to the WIS instead of passing through the DBS. But we design for the device to send the data through the DBS for the following benefits. First, it can simplify the channel device should have. A simplified communication channel can narrow the attack surface of the service. Second, this design can guarantee cooperation between DBS and WIS. Third, if the device connects DBS and WIS sequentially, it may increase the total round trip time. Because generally, Android device uses a wireless connection, but DBS and WIS are the servers with a high speed wired network.
Ⅳ. Implementation
This section covers the implementation of the remote unlocking service.
A. Security Requirements
The security algorithms used by the remote unlocking service require sufficient security strengths. Thus, we follow the recommendations of the NIST [19]. Table Ⅰ shows the requirements of the cryptographic algorithms applied to the remote unlocking service. RUApp has the X.509 certificates from the DBS and the WIS as its raw assets. The certificates containing the public key can be changed through app updates. An RPTkn and a DevNonce are generated using the SecureRandom module of Java software development kit (SDK), which complies with FIPS 140-2 security requirements [20]. TLS 1.2 or higher is used for the communications between the RUApp and the DBS. The trust anchor of the server certificates must reach one of the root CA certificates stored in Android CredentialStorage.
B. Application Signing
RUApp needs the system privilege. Thus, we wrote the Android.mk build file for RUApp, which is to be signed with the Android platform key at the build time. In this way, the Android security features mentioned in Section Ⅱ.B, Section Ⅱ.C, and Section Ⅱ.D can be applied.
C. Hide Annotation
We add the hide annotation (@hide) to the DPM's remote unlocking service APIs to hide them from the SDK [21]. From Android 9 (API level 28), the APIs with the hide annotation can only be called by an app with system privileges [22]. Since RUApp is signed with the platform key, it can call the remote unlocking service APIs. In contrast, third-party apps are not allowed to call these APIs.
D. Call Stack Monitoring
This feature restricts other system privilege apps on the device from calling the remote unlocking service APIs. Thus, we can prevent unexpected internal attacks. Table Ⅱ shows the partial code that checks the call stack and blocks API calls by arbitrary system apps. If the caller is not specified in the API, a SecurityException is thrown. Therefore, the trust boundary is minimized.
E. Custom Permission
We add custom permission to RUApp to regulate arbitrary accesses from third-party apps. Moreover, even system apps cannot access RUApp unless its custom permission is explicitly declared in their AndroidManifest.xml file. Thus, it can guarantee accountability. Table Ⅲ shows a partial code of the custom permission declared in AndroidManifest.xml of RUApp.
F. Secure Protocol
TLS protects the communication between the RUApp and the DBS. On top of TLS, we add multi-layered security mechanisms to preserve the hardware-backed security level. Figures Ⅲ and Ⅳ show our secure protocol. The payload format is the JavaScript Object Notation (JSON) type, which consists of field-value pairs. Therefore, it can be flexibly expanded without the restriction of order and length. To represent all values as human-readable characters, we use Base64 encoding if necessary. Those human-readable characters make it easy to debug and respond to security incidents. Also, Base64 encoding is able to encode arbitrary binary data into a channel that is not "8-bit clean" (i.e., not any 8-bit character is allowed on the channel). The major fields in the payload are as follows.
1) Magic: Opening ports can be sensitive for server administrators. The DBS administrator opens only ports with security countermeasures such as network firewall and intrusion protection system (IPS). That is, the DBS may use the secure port for multiple purposes. This field value specifies that an arriving packet at the port of the DBS is for the remote unlocking service.
2) Version: This represents the remote unlocking service version known to the device. Depending on the update level of the device, the version of the remote unlocking service can vary. Also, new fields can be added as the version goes up. The DBS must be able to provide the service for the version the device knows. This field allows forward and backward compatibility to be achieved.
3) DevNonce: RUApp generates a new random value in the DevNonce field value every time it sends a request packet. The DBS signs the corresponding response, including this random value. When RUApp receives the response from the DBS, it verifies the signature DBSSign with the RSA public key of the DBS. RUApp keeps the DevNonce values generated in the current session. Thus, to prevent the replay attack, RUApp drops the response from the DBS if the DevNonce is not matched.
4) DBSAlias & WISAlias: This field serves as the index of the server's public/private key pairs. If the device has received the new certificate of the server and uses the new public key, this field value lets the server know which public key is used in the payload.
5) RsaEncrypted: This field is for an RSA ciphertext. Its plaintext may contain a CMD representing the device message (e.g., RPTkn request), DevId, AES encrypted RPTkn, and USAcnt.
6) ToWIS: This field is passed to the WIS by the DBS. It contains the WISAlias, which indicates the RSA public key of the WIS that the device uses. It also includes the RSA encrypted USAcnt in the registration phase. Since the USAcnt is encrypted with the public key of the WIS, the DBS cannot see the USAcnt of the device.
7) ToBeSigned: The response includes the device-issued DevNonce and the CMD containing the server message (e.g., RPTkn response). The AES encrypted RPTkn is also included when the user requests remote unlocking via the WIS.
8) DBSSign: This field has the signature for the values in the ToBeSigned field. This is generated using the DBS RSA private key. Since ToBeSigned includes DevNonce, every response has a different signature that defends against the replay attack.
9) FromWIS: The WIS passes this field to RUApp through the DBS. This field contains the WISTimeStamp and the signature WISSign, which proves the integrity of the USAcnt of the user whose authentication succeeds. WISSign is generated by signing the USAcnt concatenated by WISTimeStamp. Thus, the WISSign is different every time. Also, as the plaintext USAcnt is not included, the DBS cannot know the USAcnt of the device.
In the device registration phase, the secure protocol works in a single transaction as shown in Figure Ⅲ. However, in the device unlocking phase, the secure protocol requires server polling for synchronization as follows. The user calls RUApp on the throttling screen. According to the user agreement, the device enables its network connectivity. The device enters the remote unlocking standby state and requests a remote unlocking payload (the black arrows in Figure Ⅲ) at regular intervals to the DBS. Until the user makes an unlocking request via the WIS, the response using CMD from the DBS is "wait." (the grey arrow in Figure Ⅲ) [23].
Once the user request is valid at the WIS, it creates a FromWIS and sends it to the DBS. The DBS completes the payload (the green arrow in Figure Ⅳ) and sends it to RUApp. Then, RUApp tries unlocking the device and sends its result (the blue arrow in Figure Ⅳ) to the DBS. The DBS sends the received result to the WIS, which displays the unlocking result to the WIS user. The detailed operations are shown in Figure Ⅳ and Section Ⅲ.C.2.
Ⅳ. Evaluation
A. Threat Analysis
We adopt the STRIDE model to identify the threats the proposed unlocking service may have. The STRIDE model is a threat modeling method that is the most mature and helps identify relevant mitigating techniques [24]. The DFDs of the registration and unlocking phases are given to Microsoft's automatic tool for the STRIDE model analysis [25] (See [A.2]). As a result, 208 possible threats from our design are identified. Next, we assess the risk level of each threat based on the OWASP risk rating [26]. Table Ⅳ summarizes the result of the threat analysis and risk assessment. We publish the whole data in [A.3].
B. Security Countermeasures
According to the result of our risk assessment as shown in [A.3], the high-level threats exist in the interactions R13, R17, U6, and U14 (see Figures Ⅰ and Ⅱ). These are in the communication channel between the RUApp and the DBS. The proposed secure protocol uses TLS, RSA, AES, and SHA256withRSA digital signature to defend against spoofing identities, tampering with data, repudiation, and information disclosure. For the medium-level threats, the device platform can be divided into a framework layer and an app layer. As to the potentially vulnerable interactions between apps, they are secured by using RUApp's Android custom permission. The DPM's remote unlocking service APIs restrict unauthorized access by leveraging application signing, hide annotation, and call-stack monitoring. To secure interactions R2 and U9, the account server utilizes OAuth 2.0. For the interaction U8, the WIS can lock the USAcnt in the case of multiple login failures to protect against the brute force attack [27]. As a result, our security design takes security countermeasures against all the high-level threats and most of the medium-level threats.
Ⅵ. Related work
As mentioned in section Ⅰ, this is the first paper that handles the Android SP. Utilizing the SP, we propose a new remote unlocking service over the current offline Android unlocking system. Also, we seek to preserve the current Android security level based on applying Android security features and inventing new security mechanisms. Thus, this paper doesn't open potential vulnerabilities in Android security.
Android security has been enhanced as its version grows. Therefore, the previous security issues mentioned in related works may not works for now. Also, considering that well-known formula "likelihood x impact" in the risk assessment step of various threat modelings, the Android security issues in the related works can be assessed differently up to its cases. So, we overview the previous researches about Android security and compare them with our research briefly.
Hassan Khan et al. proposed an implicit authentication framework for Android [28]. Their study starts with the survey result that about 53% of Android users do not use the screen lock of the Android in 2013. Their research can improve the Android security for the users who do not use the screen lock. On the contrary, our study focuses on the users who set a passphrase for their Android devices.
Jie Huang et al. studied the privacy issue in the Android accessibility service [29]. The accessibility service is a valuable function that helps people with disabilities. But, some features of the Android accessibility service can be abused. Thus, they proposed a secure accessibility service. On the contrary, our study utilizes the DPM of android and focuses on the newly designed remote unlocking service.
Muhammad Shahzad et al. proposed a gesture-based Android unlocking mechanism [30]. They claim that the Android screen lock is vulnerable to shoulder surfing attacks and smudge attacks. Therefore, they invent a gesture-based Android unlocking mechanism that the attacker can see but can not quickly reproduce. Their study seems similar to our research in designing a new unlocking mechanism of the Android device, but our study doesn't focus on the shoulder surfing attacks and smudge attacks.
Sebastian Uellenbeck et al. research the vulnerability that Android pattern unlocking may have [31]. Their study statistically suggested that the existing 3 x 3 pattern unlocking doesn't provide sufficient entropy. Also, they proposed an improved pattern lock mechanism via changing pattern layout. On the contrary, our study doesn't focus on the current Android pattern unlocking.
Timothy J. Forman et al. also proposed a new Android pattern unlocking [32]. They invent Double Patterns (DPatts) to improve the entropy of the Android pattern unlocking. But, as mentioned, our study doesn't focus on the current Android pattern unlocking.
Muhammad Rehman Zafar et al. analyzed fingerprint authentication for smart devices [33]. Their research suggested more classified levels are needed in designing fingerprint authentication for security. On the contrary, our research does not focus on biometric authentication mechanisms.
Lukas Janik et al. invented a two-factor authentication that uses an additional simple game on existing Android pattern unlocking to improve the security level [34]. In the game, behavioral biometrics-based on touch screen interaction provides secondary authentication. On the contrary, our unlocking service does not rely on behavioral biometrics.
Fadi Aloul et al. proposed two-factor authentication that uses the OTP via SMS [35]. Due to the SMS that cannot be used while the device is locked, their mechanism seems unusable for unlocking devices. On the contrary, our proposed two-factor authentication scheme focuses on device unlocking.
Ammar H. Ali et al. designed an Android app to provide secure chatting [36]. Their design uses ECDH, AES, and RC4 ciphers. On the contrary, our design utilizes RSA, AES, and SHA256withRSA ciphers that meet the NIST recommendations.
Junsung Cho et al. opened a vulnerability on Android 5.1 (Lollipop) that an attacker can unlock the arbitrary Android device [37]. Their scheme uses Firebase push message to send an attack payload. Also, a Brute force attack is conducted on the victim's screen lock. But, their attacking scheme is expected to be outdated for now. Because the gatekeeper throttles the brute force attack targeting the screen lock. Also, FBE doesn't allow the Firebase push message until the device is unlocked.
Ⅶ. Conclusion
We presented a new Android remote unlocking service using the synthetic password. The proposed service can improve the user experiences while preserving the Android hardware-based security. Also, our design supports two-factor authentication, distributed authority, trust-boundary minimization, key management, and compatibility. We evaluated the security of the proposed remote unlocking service through the STRIDE model and the OWASP risk rating. We identified 208 threats and assessed each threat's risk level using public tools. We added the corresponding countermeasures to the proposed unlocking service against all the identified high-level threats. The developed remote unlocking service has been installed on commercial devices after passing quality verification and penetration tests.
Footnote & Reference
[4] Google, “Android file-based encryption.”:
https://source.android.google.cn/security/encryption/file-based
[5] Google, “Android authentication.”:
https://source.android.com/security/authentication
[8] RPTkn is also called the escrow token in the Android framework's LockSettingService sourcecode of the AOSP and other documents.
[16] If the user already saved her USAcnt in the device, R1 ~ R3 can be skipped. In addition, the USAcnt can be saved via the Settings app.
[17] If the user fails to input the correct passphrase at this time, the device registration is canceled. By this, a malicious attacker cannot arbitrarily activate the remote unlocking service.
https://doi.org/10.6028/NIST.SP.800-57pt1r5
[20] Google, “Secure random.”:
https://developer.android.com/reference/java/security/SecureRandom
[21] Google, “Hide annotation.”:
https://source.android.com/devices/architecture/aidl/aidl-annotations#hide
[22] Google, “Restrictions on non-sdk interfaces.”:
https://developer.android.com/guide/app-compatibility/restrictions-non-sdk-interfaces
[23] If the device's polling continues forever, the user's network resource could be maliciously exhausted. Thus, we define the maximum standby duration as 5 minutes. After the maximum time has elapsed, the device standby state is canceled. The user can restart the remote unlocking manually. The interval and the threshold also help the DBS to be protected against the DoS attack.
[24] N. Shevchenko, “Threat modeling: 12 available methods.” Carnegie Mellon University’s Software Engineering Institute Blog, Dec. 3, 2018:
[25] Microsoft, “Threat modeling tool.”:
https://www.microsoft.com/en-us/securityengineering/sdl/threatmodeling
Appendices
https://drive.google.com/file/d/1MUiJLG2GU53x6jQgEagU-VFWowaU_E2q
https://drive.google.com/file/d/1430prcH3Rx_Kd3TGIGZVyEhBTTQn3YVf
https://docs.google.com/spreadsheets/d/1wr7NPYgBpOH24OdeYgJB4hGTDWgJukJNfFuJ6XYb0Uw